Chapter 46
3D Surface Mesh Generation

Table of Contents

46.1   Introduction

This package provides a function template to compute a triangular mesh approximating a surface.

The meshing algorithm requires to know the surface to be meshed only through an oracle able to tell whether a given segment, line or ray intersects the surface or not and to compute an intersection point if any. This feature makes the package generic enough to be applied in a wide variety of situations. For instance, it can be used to mesh implicit surfaces described as the zero level set of some function. It may also be used in the field of medical imaging to mesh surfaces described as a gray level set in a three dimensional image.

The meshing algorithm is based on the notion of the restricted Delaunay triangulation. Basically the algorithm computes a set of sample points on the surface, and extract an interpolating surface mesh from the three dimensional triangulation of these sample points. Points are iteratively added to the sample, as in a Delaunay refinement process, until some size and shape criteria on the elements of the surface mesh are satisfied.

The size and shape criteria guide the behavior of the refinement process and control its termination. They also condition the size and shape of the elements in the final mesh. Naturally, those criteria can be customized to satisfy the user needs. The Surface mesh generation package offers a set of standard criteria that can be scaled through three numerical values. Also the user can also plug in its own set of refinement criteria.

There is no restriction on the topology and number of components of the surface provided that the oracle (or the user) is able to provide one initial sample point on each connected component. If the surface is smooth enough, and if the size criteria are small enough, the algorithm guarantees that the output mesh is homeomorphic to the surface, and is within a small bounded distance (Hausdorff or even Frechet distance) from the surface. The algorithm can also be used for non smooth surfaces but then there is no guarantee.

46.2   The Surface Mesh Generator Interface for Smooth Surfaces

The template parameter SurfaceMeshC2T3 stands for a data structure type that is used to store the surface mesh. This type is required to be a model of the concept SurfaceMeshComplex_2InTriangulation_3. Such a data structure has a pointer to a three dimensional triangulation and encodes the surface mesh as a subset of facets in this triangulation. An argument of type SurfaceMeshC2T3 is passed by reference to the meshing function. This argument holds the output mesh at the end of the process.

The template parameter Surface stands for the surface type. This type has to be a model of the concept Surface_3.

The knowledge on the surface, required by the surface mesh generator is encapsulated in a traits class. Actually, the mesh generator accesses the surface to be meshed through this traits class only. The traits class is required to be a model of the concept SurfaceMeshTraits_3. The difference between the two overloaded versions of make_surface_mesh can be explained as follows

• In the first overloaded version of make_surface_mesh, the surface type is given as template parameter (Surface) and the surface to be meshed is passed as parameter to the mesh generator. In that case the surface mesh generator traits type is automatically generated form the surface type by an auxiliary class called the Surface_mesh_traits_generator_3.
• In the second overloaded version of make_surface_mesh, the surface mesh generator traits type is provided by the template parameter SurfaceMeshTraits_3 and the surface type is obtained from this traits type. Both a surface and a traits are passed to the mesh generator as arguments.

The first overloaded version can be used whenever the surface type either provides a nested type Surface::Surface_mesher_traits_3 that is a model of SurfaceMeshTraits_3 or is a surface type for which a specialization of the traits generator Surface_mesh_traits_generator_3<Surface> is provided. Currently, the library provides partial specializations of Surface_mesher_traits_generator_3<Surface> for implicit surfaces (Implicit_surface_3<Traits, Function>) and gray level images (Gray_level_image_3<FT, Point>).

The parameter criteria handles the description of the size and shape criteria driving the meshing process. The template parameter FacetsCriteria has to be instantiated by a model of the concept SurfaceMeshFacetsCriteria.

The parameter Tag is a tag whose type influences the behavior of the meshing algorithm. For instance, this parameter can be used to enforce the manifold property of the output mesh while avoiding an over-refinement of the mesh. Further details on this subject are given in Section 46.4.

A call to make_surface_mesh(c2t3,surface, criteria, tag) launches the meshing process with an initial set of points which is the union of two subsets: the set of vertices in the initial triangulation pointed to by c2t3, and a set of points provided by the Compute_initial_points() functor of the traits class. This initial set of points is required to include at least one point on each connected component of the surface to be meshed.

46.3   Examples

46.3.1   Meshing an Implicit Surface

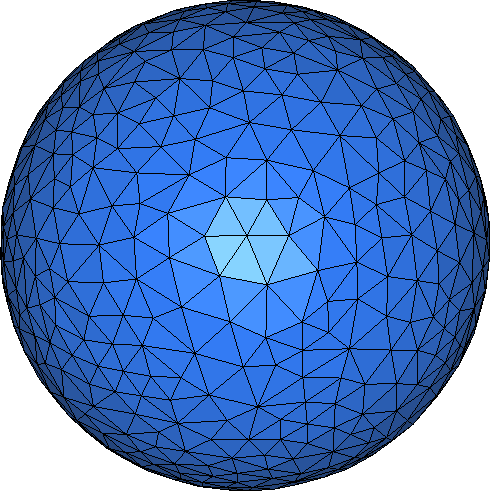
The first code example meshes a sphere given as the zero level set of a function ℝ³ → ℝ. More precisely, the surface to be meshed is created by the constructor of the class Implicit_surface_3<Kernel, Function> from a pointer to the function (sphere_function) and a bounding sphere.

The default meshing criteria are determined by three numerical values:

• angular_bound is a lower bound in degrees for the angles of mesh facets.
• radius_bound is an upper bound on the radii of surface Delaunay balls. A surface Delaunay ball is a ball circumscribing a mesh facet and centered on the surface.
• distance_bound is an upper bound for the distance between the circumcenter of a mesh facet and the center of a surface Delaunay ball of this facet.

Given this surface type, the surface mesh generator will use an automatically generated traits class.

The resulting mesh is shown in Figure 46.1.

File: examples/Surface_mesher/mesh_an_implicit_function.cpp

#include <CGAL/Surface_mesh_default_triangulation_3.h>
#include <CGAL/Complex_2_in_triangulation_3.h>
#include <CGAL/make_surface_mesh.h>
#include <CGAL/Implicit_surface_3.h>

// default triangulation for Surface_mesher
typedef CGAL::Surface_mesh_default_triangulation_3 Tr;

// c2t3
typedef CGAL::Complex_2_in_triangulation_3<Tr> C2t3;

typedef Tr::Geom_traits GT;
typedef GT::Sphere_3 Sphere_3;
typedef GT::Point_3 Point_3;
typedef GT::FT FT;

typedef FT (*Function)(Point_3);

typedef CGAL::Implicit_surface_3<GT, Function> Surface_3;

FT sphere_function (Point_3 p) {
  const FT x2=p.x()*p.x(), y2=p.y()*p.y(), z2=p.z()*p.z();
  return x2+y2+z2-1;
}

int main() {
  Tr tr;            // 3D-Delaunay triangulation
  C2t3 c2t3 (tr);   // 2D-complex in 3D-Delaunay triangulation

  // defining the surface
  Surface_3 surface(sphere_function,             // pointer to function
                    Sphere_3(CGAL::ORIGIN, 2.)); // bounding sphere
  // Note that "2." above is the *squared* radius of the bounding sphere!

  // defining meshing criteria
  CGAL::Surface_mesh_default_criteria_3<Tr> criteria(30.,  // angular bound
                                                     0.1,  // radius bound
                                                     0.1); // distance bound
  // meshing surface
  CGAL::make_surface_mesh(c2t3, surface, criteria, CGAL::Non_manifold_tag());

  std::cout << "Final number of points: " << tr.number_of_vertices() << "\n";
}

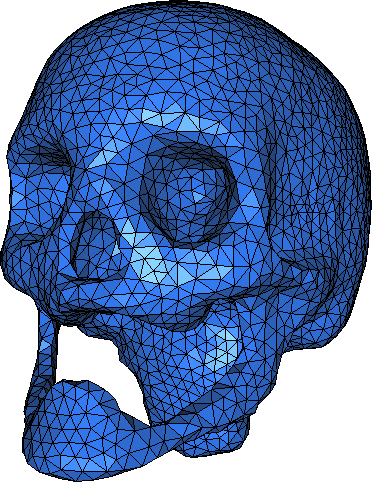
46.3.2   Meshing a Surface Defined as a Gray Level in a 3D Image

The main difference with the previous code is that the function used to define the surface is an object of type CGAL::Gray_level_image_3 created from an image file and a numerical value that is the gray value of the level one wishes to mesh.

Note that surface, which is still an object of type Implicit_surface_3 is now, defined by three parameters that are the function, the bounding sphere and a numerical value called the precision. This precision, whose value is relative to the bounding sphere radius, is used in the intersection computation. This parameter has a default which was used in the previous example. Also note that the center of the bounding sphere is required to be internal a point where the function has a negative value.

The chosen iso-value of this 3D image corresponds to a head skull. The resulting mesh is shown in Figure 46.2.

File: examples/Surface_mesher/mesh_a_3d_gray_image.cpp

#include <CGAL/Surface_mesh_default_triangulation_3.h>
#include <CGAL/Surface_mesh_default_criteria_3.h>
#include <CGAL/Complex_2_in_triangulation_3.h>
#include <CGAL/IO/Complex_2_in_triangulation_3_file_writer.h>
#include <fstream>
#include <CGAL/make_surface_mesh.h>
#include <CGAL/Gray_level_image_3.h>
#include <CGAL/Implicit_surface_3.h>

// default triangulation for Surface_mesher
typedef CGAL::Surface_mesh_default_triangulation_3 Tr;

// c2t3
typedef CGAL::Complex_2_in_triangulation_3<Tr> C2t3;

typedef Tr::Geom_traits GT;
typedef CGAL::Gray_level_image_3<GT::FT, GT::Point_3> Gray_level_image;
typedef CGAL::Implicit_surface_3<GT, Gray_level_image> Surface_3;

int main() {
  Tr tr;            // 3D-Delaunay triangulation
  C2t3 c2t3 (tr);   // 2D-complex in 3D-Delaunay triangulation

  // the 'function' is a 3D gray level image
  Gray_level_image image("data/skull_2.9.inr", 2.9);

  // Carefully choosen bounding sphere: the center must be inside the
  // surface defined by 'image' and the radius must be high enough so that
  // the sphere actually bounds the whole image.
  GT::Point_3 bounding_sphere_center(122., 102., 117.);
  GT::FT bounding_sphere_squared_radius = 200.*200.*2.;
  GT::Sphere_3 bounding_sphere(bounding_sphere_center,
                                   bounding_sphere_squared_radius);

  // definition of the surface, with 10^-5 as relative precision
  Surface_3 surface(image, bounding_sphere, 1e-5);

  // defining meshing criteria
  CGAL::Surface_mesh_default_criteria_3<Tr> criteria(30.,
                                                     5.,
                                                     5.);

  // meshing surface, with the "manifold without boundary" algorithm
  CGAL::make_surface_mesh(c2t3, surface, criteria, CGAL::Manifold_tag());
  std::ofstream out("out.off");
  CGAL::output_surface_facets_to_off (out, c2t3);
  std::cout << "Final number of points: " << tr.number_of_vertices() << "\n";
}

46.4   Meshing Criteria, Guarantees and Variations

The guarantees on the output mesh depend on the mesh criteria. Theoretical guarantees are given in [BO05]. First, the meshing algorithm is proved to terminate if the lower bound on facets angles is not bigger than 30 degrees. Furthermore, the output mesh is guaranteed to be homeomorphic to the surface, and there is a guaranteed bound on the distance (Hausdorff and even Frechet distance) between the mesh and the surface if the radius bound is everywhere smaller than the ε times the local feature size. Here ε is a constant that has to be less than 0.16, and the local feature size lfs(x) is defined on each point x of the surface as the distance from x to the medial axis. Note that the radius bound need not be uniform, although it is a uniform bound in the default criteria.

Naturally, such a theoretical guarantee can be only achieved for smooth surfaces that have a finite, non zero reach value. (The reach of a surface is the minimum value of local feature size on this surface).

The value of the local feature size on any point of the surface or its minimum on the surface it usually unknown although it can sometimes be guessed. Also it happens frequently that setting the meshing criteria so as to fulfill the theoretical conditions yields an over refined mesh. On the other hand, when the size criteria are relaxed, no homeomorphism with the input surface is guaranteed, and the output mesh is not even guaranteed to be manifold. To remedy this problem and give a more flexible meshing algorithm, the function template make_surface_mesh has a tag template parameter allowing to slightly change the behavior of the refinement process. This feature allows, for instance, to run the meshing algorithm with a relaxed size criteria, more coherent with the size of the mesh expected by the user, and still have a guarantee that the output mesh forms a manifold surface. The function make_surface_mesh has specialized versions for the following tag types:
Manifold_tag: the output mesh is guaranteed to be a manifold surface without boundary.
Manifold_with_boundary_tag: the output mesh is guaranteed to be manifold but may have boundaries.
Non_manifold_tag: the algorithm relies on the given criteria and guarantees nothing else.

46.5   Output

This Cgal component also provides functions to write the reconstructed surface mesh to the Object File Format (OFF) [Phi96] and to convert it to a polyhedron (when it is manifold):
CGAL::output_surface_facets_to_off
CGAL::output_surface_facets_to_polyhedron

46.6   Undocumented Features Available in Demos

The Polyhedron demo has a feature that allows to remesh a polyhedral surface, using the 3D Surface Mesh Generator. That has been implemented as a special model of SurfaceMeshTraits_3, for polyhedra. That traits class is not yet documented because its interface and code have not yet been stabilized. It will probably be shipped with next release of Cgal.

The Surface Mesh Generator demo allows to mesh not only gray level images, but also segmented images, when voxels are labelled with a domain index. Such images are for example the result of a segmentation of 3D medical images. This feature is not yet ready to be documented in current release, but will probably be in next release of Cgal.

46.7   Design and Implementation History

The algorithm implemented in this package is mainly based on the work of Jean-Daniel Boissonnat and Steve Oudot [BO05]. Steve Oudot implemented a first working prototype of the algorithm during his PhD thesis.

The meshing algorithm is implemented using the design of mesher levels described in [RY07].

David Rey, Steve Oudot and Andreas Fabri have participated in the development of this package.